728x90
1. 합이 10인 부분집합 구하기 ( 모든 경우 확인)
def f(i,N,K): # i부분집합에 포함될지 결정할 원소의 인덱스, N 전체 원소개수, K 찾는 합
global cnt
cnt += 1
if i == N : # 한개의 부분집합 완성
# print(bit, end=' ')
sum = 0
for j in range(N):
if bit[j]:
sum += a[j]
if sum == K: # 찾는 합이면
for j in range(N):
if bit[j]:
print(a[j], end=' ')
print()
else:
bit[i] = 1
f(i+1,N,K)
bit[i] = 0
f(i+1,N,K)
return
a = [1,2,3,4,5,6,7,8,9,10]
N = len(a)
bit = [0]*N
cnt = 0
f(0,N,10)
print('cnt = ',cnt) # 모든 경우를 확인 cnt는 항상 2047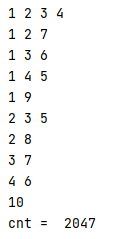
2. 합이 10인 부분집합 구하기 (조건 추가 : 더 이상 고려할 원소가 없을 때, 합이 목표 초과할 때)
# i 부분집합에 포함될지 결정할 원소의 인덱스, N 전체 원소개수, s 이전까지 고려된 원소의 합, t 목표값
def f(i,N,s,t):
global cnt
cnt += 1
if s == t: # 목표값을 찾으면
for j in range(N):
if bit[j]:
print(a[j],end=' ')
print()
elif i == N: # 더 이상 고려할 원소가 없으면
return
elif s > t: # 고려한 원소의 합 s가 이미 목표를 초과한 경우
return
else:
bit[i] = 1
f(i+1,N,s+a[i],t)
bit[i] = 0
f(i+1,N,s,t)
return
N = 10
a = [x for x in range(1,N+1)]
bit = [0]*N
t = 10 # 찾고자 하는 합
cnt = 0
f(0,N,0,t)
print('cnt = ',cnt) # 합이 커질수록 cnt 커짐
3. 합이 10인 부분집합 구하기 (조건 추가 : 더 이상 고려할 원소가 없을 때, 합이 목표 초과할 때 + 고려하지 않은 원소들까지 다 더해도 목표에 도달하지 못할 때)
# i 부분집합에 포함될지 결정할 원소의 인덱스, N 전체 원소개수,
# s 이전까지 고려된 원소의 합, t 목표값, rs 고려하지 않은 원소들의 합
def f(i,N,s,t,rs):
global cnt
cnt += 1
if s == t: # 목표값을 찾으면
for j in range(N):
if bit[j]:
print(a[j],end=' ')
print()
elif i == N: # 더 이상 고려할 원소가 없으면
return
elif s > t: # 고려한 원소의 합 s가 이미 목표를 초과한 경우
return
elif s+rs < t:
return
else:
bit[i] = 1
f(i+1,N,s+a[i],t,rs-a[i])
bit[i] = 0
f(i+1,N,s,t,rs-a[i])
return
N = 10
a = [x for x in range(1,N+1)]
bit = [0]*N
t = 10 # 찾고자 하는 합
cnt = 0
f(0,N,0,t,sum(a))
print('cnt = ',cnt)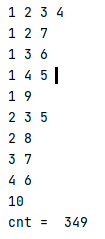
⭐ cnt 비교
합이 10인 경우
1. 2047
2. 349
3. 349
합이 27인 경우
1. 2047
2. 1645
3. 1353
합이 55인 경우
1. 2047
2. 2047
3. 21
❗
1.의 경우 모든 경우를 확인하기 때문에 항상 cnt 2047
2.의 경우 합(목표)이 커질수록 cnt 점점 커짐
3.의 경우 cnt가 커졌다가 다시 작아짐( 작아지는 시작점은 합이 (모든원소의 합 // 2)일 때)
728x90
반응형
'TIL - 프로그래밍 > 개념, 설정' 카테고리의 다른 글
| [Python] 인접 행렬,인접 리스트 만들기(pprint) (0) | 2022.03.12 |
|---|---|
| [Python] 순열, 재귀 (0) | 2022.03.08 |
| [Python] 부분집합 - 순열1 (0) | 2022.03.05 |
| [Python] 퀵 정렬 (0) | 2022.03.01 |
| [Python] 백트래킹 (Backtracking) 기법 (0) | 2022.02.28 |




댓글