728x90
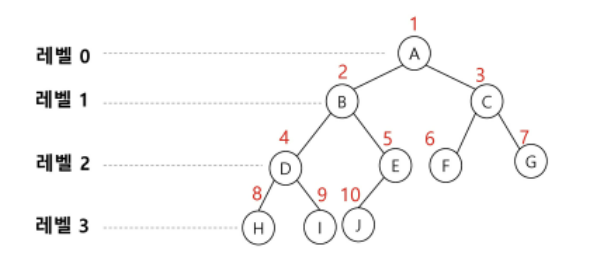
- 배열을 이용한 이진 트리 표현
- 루트 번호를 1로 함
- 레벨 n에 있는 노드에 대하여 왼쪽부터 오른쪽으로 2^n부터 2^(n+1)-1까지 번호를 차례로 부여
- 노드 번호를 배열의 인덱스로 사용
- 노드 번호의 성질
- 노드 번호가 i인 노드의 부모 노드 번호 : i//2
- 노드 번호가 i인 노드의 왼쪽 자식 노드 번호 : i*2
- 노드 번호가 i인 노드의 오른쪽 자식 노드 번호 : i*2+1
- 레벨 n의 노드 번호 시작 번호 : 2^n
- 단점
- 편향 이진 트리의 경우 사용하지 않는 배열 원소에 대한 메모리 공간 낭비 발생
- 트리의 중간에 노드를 삽입하거나 기존의 노드를 삭제할 경우 배열의 크기 변경 어려워 비효율적

- 자식 번호를 인덱스로 부모 번호를 저장
# edge 수
E = int(input()) # 4
arr = list(map(int, input().split())) # 1 2 1 3 3 4 3 5
# 정점 수 == 1번부터 V번까지 정점이 있을때 마지막 정점 번호
V = E + 1
# 자식 번호를 인덱스로 부모 번호를 저장
par = [0]*(V+1)
for i in range(E):
p,c = arr[i*2], arr[i*2+1]
par[c] = p- 루트, 조상 찾기
# root 찾기
root = 0
for i in range(1,V+1):
if par[i] == 0:
root = i
break
print(root)
# 정점 c의 조상찾기
c = 3
anc = []
while par[c] != 0:
anc.append(par[c])
c = par[c]
print(*anc)
- 연결리스트를 이용한 트리 표현
- 배열을 이용한 이진 트리 표현의 단점 보완

- 이진 트리 만들어서 전위 순회하여 정점 번호 출력
V = 13
edges = list(map(int,'1 2 1 3 2 4 3 5 3 6 4 7 5 8 5 9 6 10 6 11 7 12 11 13'.split()))
# 인덱스가 부모의 정점 번호가 되는 배열 2개 선언해서 사용
arr = [[0]*(V+1) for _ in range(2)]
tree = [0]*32
# arr[0] : 왼쪽 자식 정보
# arr[1] : 오른쪽 자식 정보
for i in range(0,len(edges),2):
# edges[i]가 부모노드 번호
# edges[i+1]이 자식 노드 번호
if arr[0][edges[i]]: # 왼쪽 자식 정보가 있으면 오른쪽 자식 설정
arr[1][edges[i]] = edges[i+1]
else:
arr[0][edges[i]] = edges[i+1]
# 만약에 부모노드가 없으면 루트
if edges[i] not in tree:
tree[1] = edges[i]
# 부모노드의 왼쪽자식이 있으면, 오른쪽 자식으로 설정
# 아니면 왼쪽 자식으로 설정
# 배열형태에서 왼쪽 자식의 인덱스를 확인하려면 부모노드의 인덱스를 알아야 함
p_idx = tree.index(edges[i])
# 왼쪽 자식의 인덱스 : 부모인덱스 * 2
# 왼쪽 자식 있으면 오른쪽에 넣기
if tree[p_idx*2]:
tree[p_idx*2+1] = edges[i+1]
else:
tree[p_idx*2] = edges[i+1]
print(tree)
# 결과
# [0, 1, 2, 3, 4, 0, 5, 6, 7, 0, 0, 0, 8, 9, 10, 11, 12, 0, 0, 0, 0,0, 0, 0, 0, 0, 0, 0, 0, 0, 13, 0]
def pre_order(v):
# arr에 정점이 없는 경우는 0으로 저장되어있음
if v != 0:
# 정점이 있다면, 작업하기 -> 전위순회
# 현재 정점 작업(출력)
print(v,end=' ')
# 왼쪽 자식 탐색
pre_order(arr[0][v])
# 오른쪽 자식 탐색
pre_order(arr[1][v])
def pre_order2(idx):
# tree에 정점이 없는 경우는 0으로 저장되어있음
if tree[idx] != 0:
# 정점이 있다면, 작업하기 -> 전위순회
# 현재 정점 작업(출력)
print(tree[idx],end=' ')
# 왼쪽 자식 탐색
pre_order(idx*2)
# 오른쪽 자식 탐색
pre_order(idx*2+1)
pre_order(1)
print()
print('----------')
pre_order2(1)
# 결과
# 1 2 4 7 12 3 5 8 9 6 10 11 13728x90
반응형
'TIL - 프로그래밍 > 개념, 설정' 카테고리의 다른 글
| [Python] 데이터베이스 (0) | 2022.04.15 |
|---|---|
| [Python] Tree3 - heap (0) | 2022.04.05 |
| [Python] Tree1 (0) | 2022.04.03 |
| [Python] 재귀로 순열, 조합 (0) | 2022.03.28 |
| [Python] 반복과 재귀 (0) | 2022.03.26 |

댓글